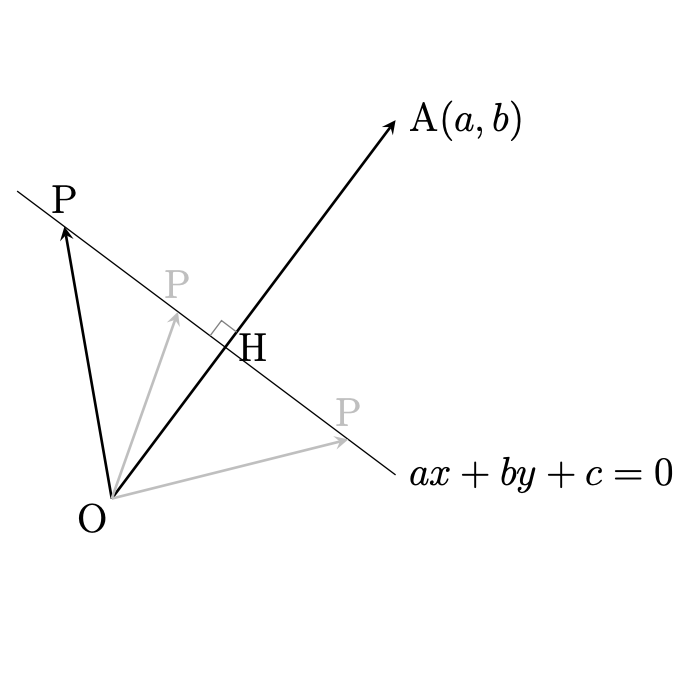
原点を\({\rm{O}}\)とする座標平面上に
定点\({\rm{A}}(a,b)\)をとる.
ある定数\(c\)があり,点\({\rm{P}}\)が,
$$\overrightarrow{\rm{OA}}\cdot\overrightarrow{\rm{OP}}=-c$$
を満たしながら動くとき,
点\({\rm{P}}\)の軌跡の方程式は,次の通りである.
$$ax+by+c=0$$
座標平面上において,
点\({\rm{A}}\)と直線\(ax+by+c=0\)の位置関係を
イメージするには,
正射影ベクトル
を考え,
内積を図形的なイメージを持つことが重要である.
直線の方程式の一般形である \(ax+by+c=0\)の形を (正確な言い方ではないが)
「定点と動点の内積が一定」
結論として, \(-c>0\)のとき, 点\({\rm{A}}\)と直線\(ax+by+c=0\)の位置関係は, 下図のようになる. ただし,\({\rm{OH}}=\displaystyle\frac{|c|}{{\rm{OA}}}\)である.