$$
e=2.71828
18284
59045
23536
02874
71352\cdots
$$
の2つの定義を紹介し,
それらが同値である事を証明する.
まずは1つ目の定義を述べる.
定義1.
極限値\(\lim_{h\to0}(1+h)^\frac{1}{h}\)が存在する
ので,
その値を\(e\)と定める.すなわち
$$
e=\lim_{h\to0}(1+h)^\frac{1}{h}
$$
と定義する.
注意.
残念ながら, \(\lim_{h\to0}(1+h)^\frac{1}{h}\) が収束することの証明は高校数学の範囲を超えてしまう. これについては, ネイピア数の定義(極限値の存在) を参照.
次に2つ目の定義を述べるための準備を行う.注意.
残念ながら, \(\lim_{h\to0}(1+h)^\frac{1}{h}\) が収束することの証明は高校数学の範囲を超えてしまう. これについては, ネイピア数の定義(極限値の存在) を参照.
\(a > 1\)とする. 関数\(y=a^x\)において, \(a\)の値に関わらず,点\((0,1)\)は,この関数上の点である. そこで, \(y=a^x\)上の点\((0,1)\)における接線の傾きが\(1\)となるような 実数\(a\)を考えることができる. \(y=a^x\)のグラフの形から, このような\(a\)がただ1つ存在することがわかる (下図を参照). \(f(x)=a^x\)とすると, \(f(x)\)は,(実数全体で)微分可能であり, 微分の定義から, $$ f'(x) =\lim_{h\to0}\frac{a^{x+h}-a^x}{h} =a^x\lim_{h\to0}\frac{a^{h}-1}{h} $$ なので, 点\((0,1)\)における接線の傾きは, $$ f'(0) =\lim_{h\to0}\frac{a^{h}-1}{h} $$ となる.
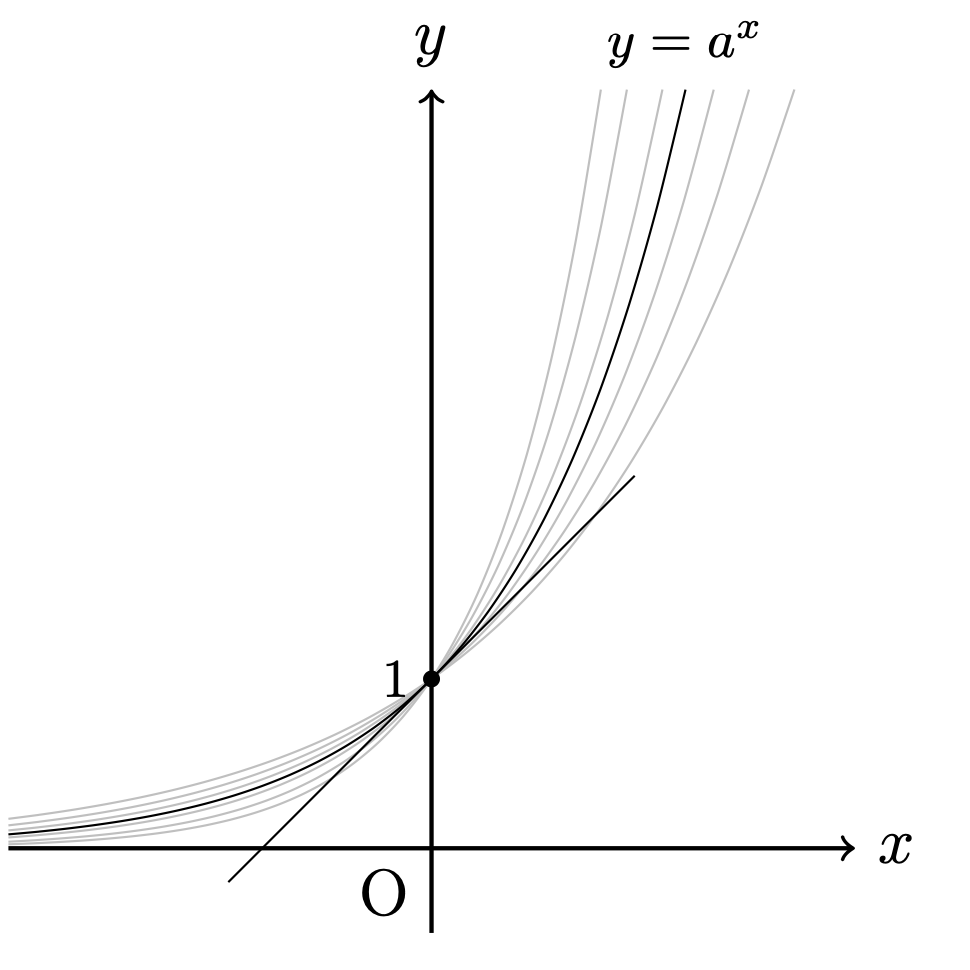
定義2.
\(a > 1\)とする.
\(y=a^x\)上の点\((0,1)\)での接線の傾きが\(1\)となるような\(a\)の値を\(e\)と定める.
すなわち,
$$
\lim_{h\to0}\frac{a^{h}-1}{h}=1
$$
を満たす\(a\)の値を\(e\)と定義する.
最後に,この2つの定義で定められる\(e\)が同じものであることを証明する.
定理.
ネイピア数の2つの定義は同値である.
すなわち,次が成り立つ.
$$
e=\lim_{h\to0}(1+h)^\frac{1}{h}
\Longleftrightarrow
\lim_{h\to0}\frac{e^{h}-1}{h}=1
$$
