命題(\(\frac{1}{30}\)公式)
定数\(\alpha,\beta\)に対して,次が成り立つ.
$$
\int_\alpha^\beta (x-\alpha)^2(x-\beta)^2\ dx
\ =\
\frac{1}{30}(\beta-\alpha)^5
$$
\(\frac{1}{30}\)公式は, 次のように言い換えることができる.
命題.
\(f(x)=ax^4+bx^3+cx^2+dx+e\ (a\ne0)\)とし,
四次曲線\(C:y=f(x)\)
が複接線を持つとする.
さらに,
\(C\)と\(\ell\)の
異なる2つの接点を
\((\alpha,f(\alpha)),\ (\beta,f(\beta))\)
とする.
このとき,
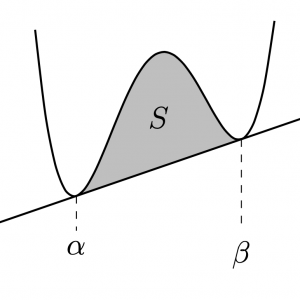
\(C\)と\(\ell\)で囲まれる部分の面積\(S\)について
次が成り立つ.
$$
S
\ =\
\frac{|a|}{30}(\beta-\alpha)^5
$$
四次関数の複接線の存在条件については コチラ.
