次の値を求めよ.
本稿の動機は,上のような問題を考えることである.
$$\sin10^\circ+\sin82^\circ+\sin154^\circ+\sin226^\circ+\sin298^\circ$$
三角関数 の 加法定理 の公式を駆使すれば解けなくもないが面倒くさい.
それよりも,\(\theta=72^\circ\)としたとき,与式が,
$$\sin10^\circ
+\sin(10^\circ+\theta)
+\sin(10^\circ+2\theta)
+\sin(10^\circ+3\theta)
+\sin(10^\circ+4\theta)$$
という形になっていることに気づけば,
(そもそも,加法定理を駆使して解ける場合はこのことに気付いていると思うが,)
自然と下のような図形が思い浮かぶはずである.
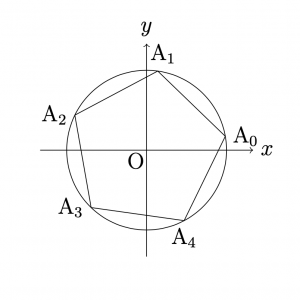
単位円上に頂点を持つ正五角形 \({\rm{A_0A_1A_2A_3A_4}}\)の頂点の\(y\)座標の和を求める問題
最後に, 同様に 単位円上に頂点を持つ正\(n\)角形を考えることで,
$$\sum_{k=0}^{n-1}\sin\left(\varphi+\frac{2k\pi}{n}\right)
=\sum_{k=0}^{n-1}\cos\left(\varphi+\frac{2k\pi}{n}\right)
=0$$
が従うことについても言及する.
