\(f(x)=x^2+bx+c\) \((b,c\in\mathbb{R})\)とし,
判別式\(D=b^2-4c\leq0\)を仮定する.
二次方程式\(f(x)=0\)の解のひとつを\(\alpha\)とするとき,
次が成り立つ.
$$
\sqrt{f(x)}
\hspace{5pt}=\hspace{5pt}\mid x-\alpha\mid
$$
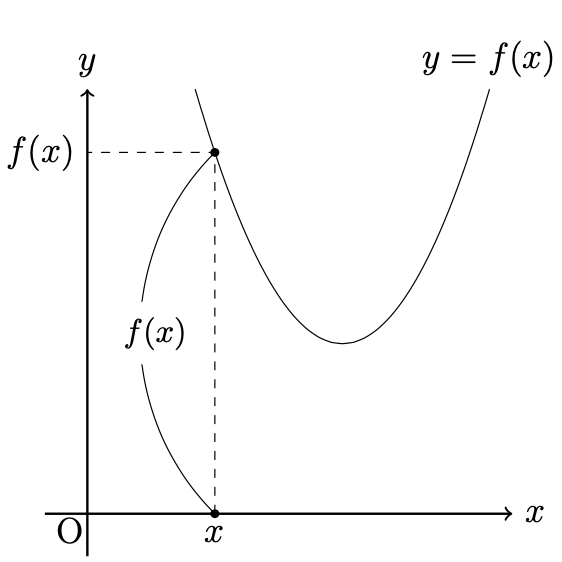
\(\sqrt{f(x)}\)は, 二次関数\(y=f(x)\)の高さ (右図を参照)の根号をとったものであり,
\(\mid x-\alpha \mid\)は, 二次方程式\(f(x)=0\)の解\(\alpha\)と, 点\(x\)との距離である.
$$\sqrt{f(x)}=\mid x-\alpha \mid$$
は,これら2つを結びつけるものと解釈すると,とても興味深い.ここでは,3次元空間を用いて, 二次方程式の虚数解を図示する ことで, このことについて解説する.

