$$
y=f(x),
\hspace{20pt}
f(x)=ax^4+bx^3+cx^2+dx+e
\hspace{10pt}(a\ne0)
$$
が
複接線を持つための必要十分条件
は,
$$
3b^2-8ac>0
$$
が成り立つことであり
,
複接線定理
から,
複接線の傾きは,
\(f^{\prime\prime\prime}(\gamma)=0\)を満たす\(\gamma\)を用いて,
$$
f'(\gamma)
$$
と書けるのであった.
また,
異なる\(2\)つの接点を
\(
\left(\alpha,f(\alpha)\right)
,\
\left(\beta,f(\beta)\right)
\)
とすると,
$$
\gamma=\frac{\alpha+\beta}{2}
$$
が成り立つのであった.
命題.
上の記号をそのまま用いる.
\(4\)次関数\(C:y=f(x)\)は,
複接線\(\ell\)を持つとする.
任意の\(u\)に対して,
\(\ell\)と傾きが等しい直線\(\ell_u\):
$$
y=\ell_u(x)
,\hspace{20pt}
\ell_u(x)=f'(\gamma)x+u
$$
を考える.
\(C\)と\(\ell_u\)が共有点を持つとき,
その共有点と,点
$${\rm{P}}_u(\gamma,\ell_u(\gamma))$$に関して
対称である点も共有点のうちの\(1\)つである.
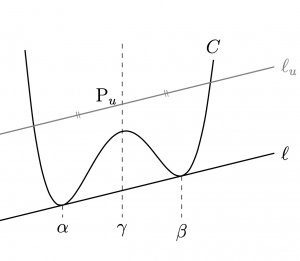

複接線を持たない\(4\)次関数に対しても, 上と同様に\(f'(\gamma)\)が定義できるので, これを傾きに持つ直線\(\ell_u\)を考えることにより, 上の命題は,複接線を持たない\(4\)次関数に対しても,成り立つ.
以上から, \(4\)次関数が,線対称になるためには, \(f'(\gamma)=0\)が必要十分であることが分かる. \(f'(\gamma)\)を計算することにより次が従う.
命題.
\(4\)次関数
$$
f(x)=ax^4+bx^3+cx^2+dx+e
\ (a\ne0)
$$
に対して,
曲線\(y=f(x)\)が線対称となるための必要十分条件は,
$$
b^3-4abc+8a^2d=0
$$
が成り立つことである.
またこのとき,
\(y=f(x)\)は,直線\(x=-\displaystyle\frac{b}{4a}\)に関して線対称である.
