放物線の準線と直交する\(2\)接線

あいだBy gleamath
座標平面において， 放物線は， 定点\({\rm{F}}\)と， \({\rm{F}}\)を通らない定直線\(\ell\)からの距離が等しい点の軌跡として定義される． このとき， 定点\({\rm{F}}\)と定直線\(\ell\)を それぞれ， 放物線の焦点と準線というのであった． 準線が座標軸と平行である場合には， 放物線の方程式は次のように表せることが知られている． 以下では，\(p,q\ne0\)とする．
  • 焦点\((p,0)\)と，準線\(x=-p\)で定義される放物線の方程式は， 次のように表せる： $$ y^2=4px. $$
  • 焦点\((0,q)\)と，準線\(y=-q\)で定義される放物線の方程式は， 次のように表せる： $$ x^2=4qy. $$
逆に放物線に対して， その準線は次のように定めることができる．
命題． \(p,q\ne0\)とする．
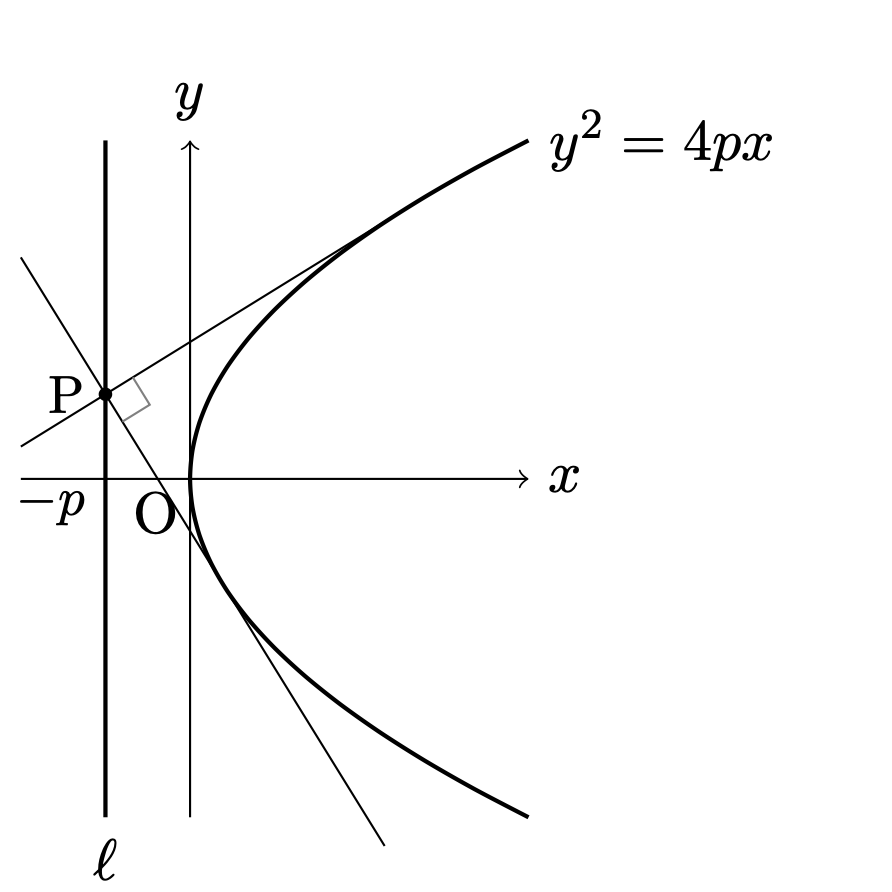
  • 放物線\(C:y^2=4px\)の直交する\(2\)接線の交点\({\rm{P}}\)の奇跡は，準線\(x=-p\)である．
  • 放物線\(C’:x^2=4qx\)の直交する\(2\)接線の交点\({\rm{Q}}\)の奇跡は，準線\(y=-q\)である．


命題の証明はコチラ
PDF