定理.
結果は,それぞれ,
楕円の外から引いた接線の直交条件,
双曲線の外部の点から引いた接線の直交条件
から,従う.
- 楕円 \(\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) の直交する\(2\)接線の交点の軌跡は, 円 $$x^2+y^2=a^2+b^2$$である.
-
双曲線
\(\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=\pm1\)
の直交する\(2\)接線の交点の軌跡は,
$$
x^2+y^2=\pm(a^2-b^2)
$$
である.
ただし,
漸近線\(y=\pm\displaystyle\frac{b}{a}x\)上の\(4\)点は除く.
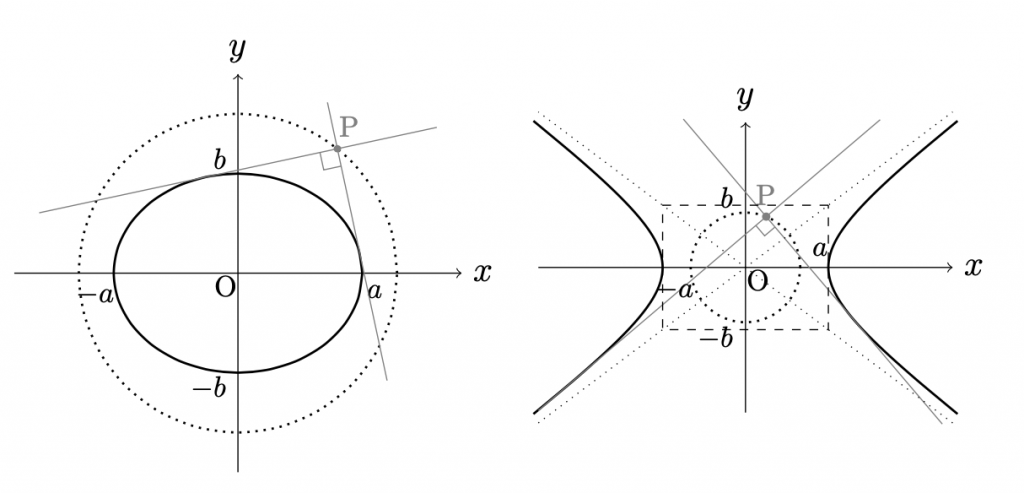
定義. 上の命題の軌跡を, 楕円(または双曲線)の準円 という.
