円と点に対して決まる次の値のことを 方べき(の値)という.
\((\) 点と円の中心の距離 \()^2\hspace{5pt}-\hspace{5pt}(\) 円の半径 \()^2\)
よく知られた次の2つの定理は, その値が,
方べきの値に等しい
(ただし,点\({\rm{P}}\)が円の内部にある時は, 方べきの値の\(-1\)倍に等しい)
方べきの定理1
点\({\rm{P}}\)を通る2直線が, 円とそれぞれ 2点\({\rm{A}}\),\({\rm{B}}\)と 2点\({\rm{C}}\),\({\rm{D}}\)で交わっている時, $${\rm{PA}}\cdot{\rm{PB}}={\rm{PC}}\cdot{\rm{PD}}$$ が成り立つ.
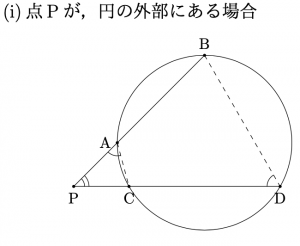
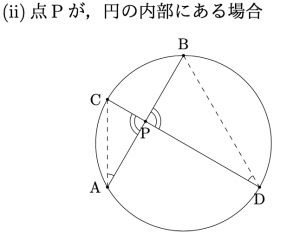
方べきの定理2
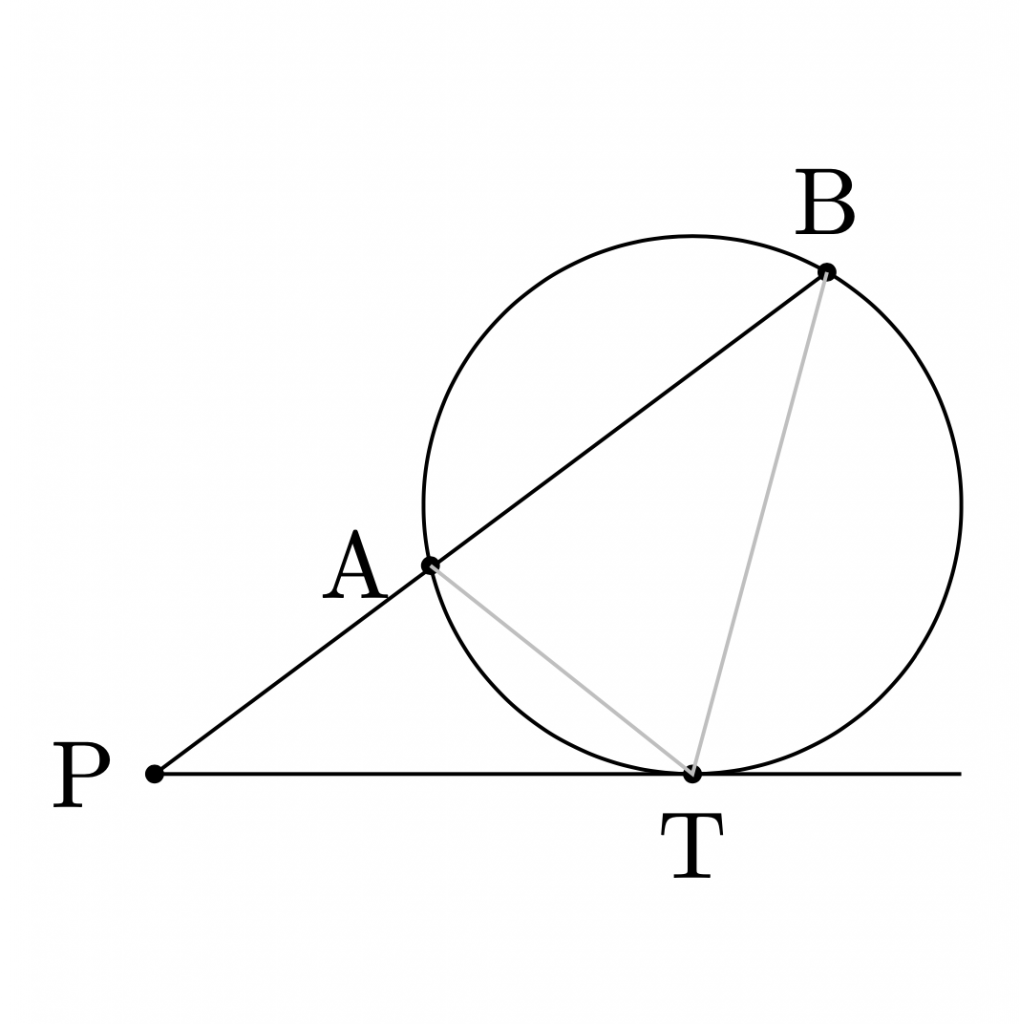
円の外にある点\({\rm{P}}\)を通る2直線の一方が, 円と2点\({\rm{A}}\),\({\rm{B}}\)で交わり, もう一方が 点\({\rm{T}}\)で接している時, $${\rm{PA}}\cdot{\rm{PB}}={\rm{PT}}^2$$ が成り立つ.
また,次の方べきの定理の逆についても証明する.
方べきの定理の逆
- 2つの線分\({\rm{AB}}\),\({\rm{CD}}\), またはそれらの延長線どうしが 点\({\rm{P}}\)で交わり, $${\rm{PA}}\cdot{\rm{PB}}={\rm{PC}}\cdot{\rm{PD}}$$ が成り立つなら, 4点\({\rm{A, B, C, D}}\)は, 同一円周上にある.
- 円の弦\({\rm{AB}}\)の延長線上の点\({\rm{P}}\)と その円周上の点\({\rm{T}}\)に対して, $${\rm{PA}}\cdot{\rm{PB}}={\rm{PT}}^2$$ が成り立つなら, \({\rm{PT}}\)はこの円に接する.
