アポロニウスの円とメネラウスの定理

高校数学By gleamath
\(\bigtriangleup{\rm{ABC}}\)と， 互いに異なる 正の実数\(a,b,c\)に対して，
  • 頂点\({\rm{A,B}}\)からの距離の比がそれぞれ\(a:b\)である点の軌跡を\(\Gamma_1\)，
  • 頂点\({\rm{B,C}}\)からの距離の比がそれぞれ\(b:c\)である点の軌跡を\(\Gamma_2\)，
  • 頂点\({\rm{C,A}}\)からの距離の比がそれぞれ\(c:a\)である点の軌跡を\(\Gamma_3\)
と定めると， 図形\(\Gamma_i\ (i=1,2,3)\)は全て円 であることが知られている （アポロニウスの円）
そこで， その中心をそれぞれ\({\rm{O}}_i\ (i=1,2,3)\)とすると， 次が成り立つ．
命題． ３点\({\rm{O}}_i\ (i=1,2,3)\)は一直線上にある． （下図は，\(a > b > c\)の場合）
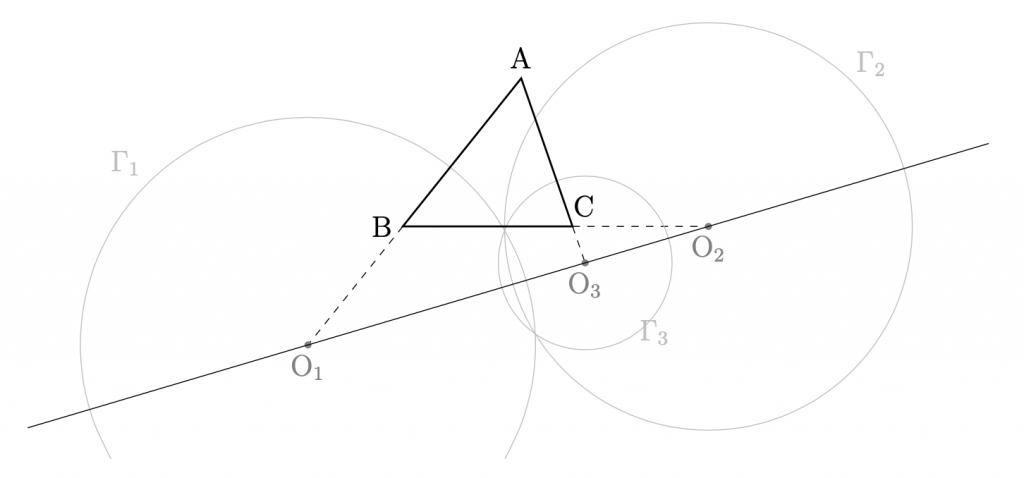
証明には， メネラウスの定理の逆を用いる．
PDF