アポロニウスの円と根軸

あいだBy gleamath
\(\bigtriangleup{\rm{ABC}}\)と， 互いに異なる 正の実数\(a,b,c\)に対して，
  • 頂点\({\rm{A,B}}\)からの距離の比がそれぞれ\(a:b\)である点の軌跡を\(\Gamma_1\)，
  • 頂点\({\rm{B,C}}\)からの距離の比がそれぞれ\(b:c\)である点の軌跡を\(\Gamma_2\)，
  • 頂点\({\rm{C,A}}\)からの距離の比がそれぞれ\(c:a\)である点の軌跡を\(\Gamma_3\)
と定めると， 図形\(\Gamma_i\ (i=1,2,3)\)は全て円 であることが知られている （アポロニウスの円）
そこで， その中心と半径をそれぞれ\({\rm{O}}_i\ (i=1,2,3)\)， \(r_i\ (i=1,2,3)\)とし， ２円\(\Gamma_i,\Gamma_j\ (i=1,2,3,\ j=1,2,3,\ i\ne j)\)の 根軸を \(\ell(i,j)\)と表す． このとき，次が成り立つ．
命題．
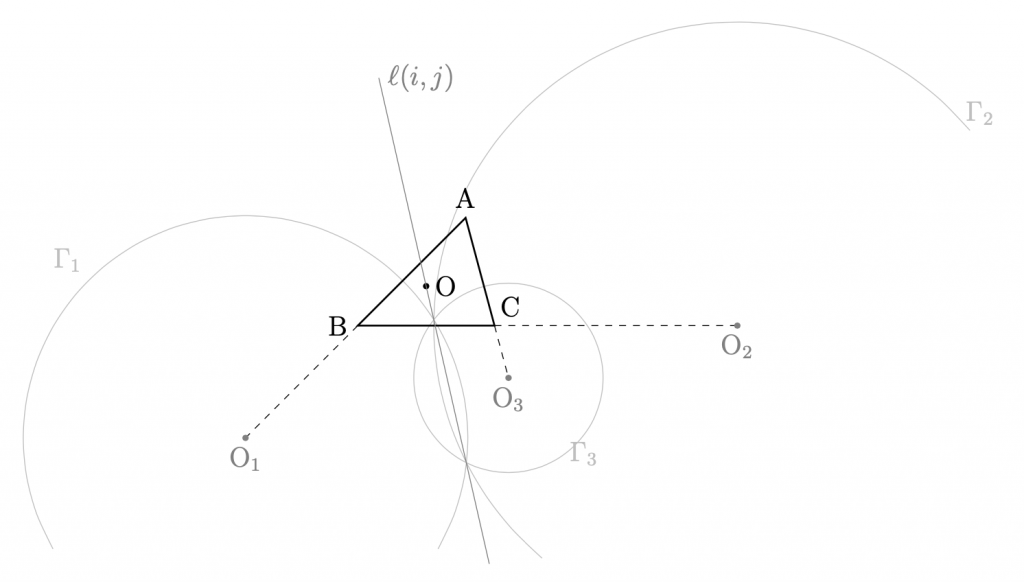
  1. 根軸\(\ell(i,j)\)は全て一致し，\(\bigtriangleup{\rm{ABC}}\)の外心\({\rm{O}}\)を通る．
  2. ３円\(\Gamma_i\ (i=1,2,3)\)のうち， ２つが共有点を持つなら，もう１つもその共有点を通る．

PDF


この記事は， [数学セミナー2020.11] を参考にさせていただいています．