命題.
微分可能な関数\(y=f(x)\)と,その定義域内の区間\(I\)において,
次が成り立つ.
次の命題は,極値の判定に便利である.
- 全ての\(x\in I\)に対して \(f^{\prime\prime}(x) > 0\) ならば, \(f(x)\)は\(I\)で下に凸である.
- 全ての\(x\in I\)に対して \(f^{\prime\prime}(x) < 0\) ならば, \(f(x)\)は\(I\)で上に凸である.
命題.
微分可能な関数\(f(x)\)において,
\(x=a\)の十分近くの区間で\(f^{\prime\prime}(x)\)が連続であるとする.
このとき,次が成り立つ.
- \(f'(a)=0\)かつ\(f^{\prime\prime}(a) > a\)ならば, \(f(a)\)は極小値である.
- \(f'(a)=0\)かつ\(f^{\prime\prime}(a) < a\)ならば, \(f(a)\)は極大値である.
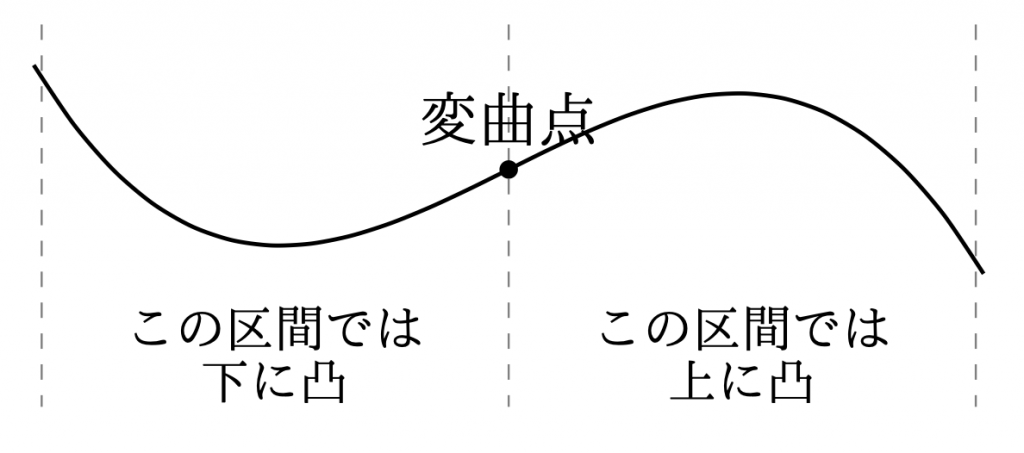
さらに,下に凸と上に凸が変わる境目の点として変曲点を定義し, 次の2つの命題を証明する.
命題.
微分可能な関数\(y=f(x)\)上の点\({\rm{P}}(a, f(a))\)に対して,
\(x=a\)の前後で,\(f^{\prime\prime}(x)\)の符号が変わるならば,
点\({\rm{P}}\)は変曲点である.
命題.
微分可能な関数\(y=f(x)\)上の点\({\rm{P}}(a, f(a))\)に対して,次が成り立つ.
点\({\rm{P}}\)が変曲点
\(\Longrightarrow\)
\(f^{\prime\prime}(a)=0\)