$$
C:y=f(x)
,\hspace{20pt}
f(x)=ax^4+bx^3+cx^2+dx+e
\hspace{10pt}
(a\ne0)
$$
のみを考える
(4次関数の複接線の存在条件)
.
曲線\(C\)と複接線の傾きについて,
次が成り立つ.
定理(複接線定理).
曲線
\(C:y=f(x)\)が
複接線\(\ell\)を持つとする.
このとき,
\(f^{\prime\prime\prime}(\gamma)=0\)が成り立つような
\(\gamma\)に対して,
\(f'(\gamma)\)は,
複接線\(\ell\)の傾きである.
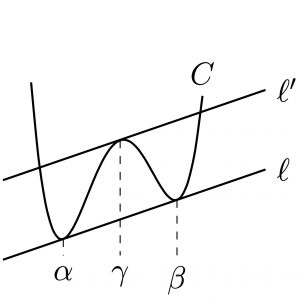

補足. 複接線の傾きは, 4次関数の対称性 と関係が深い.
