$$
f(x)=ax^4+bx^3+cx^2+dx+e\hspace{10pt}
(a\ne0)
$$
において,
曲線\(C:y=f(x)\)
が,
複接線を持つための必要十分条件
は,
$$
D:=3b^2-8ac>0
$$
が成り立つことであった.
以下では,\(D>0\)を仮定する.
4次曲線\(C\)に対して,その複接線\(\ell\)はただ1つに決まることから, \(C\)と\(\ell\)で囲まれる部分の面積も, \(C\)の方程式のみによって決まることが分かる. この事実と, 1/30面積公式 を合わせることで, 次の公式を得ることができる.
\(f(x)=ax^4+bx^3+cx^2+dx+e,\ (a\ne0)\)とし,
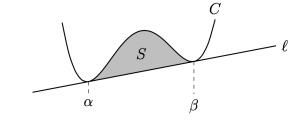
曲線\(C:y=f(x)\)が複接線\(\ell\)を持つとする.
このとき,
\(C\)と\(\ell\)で囲まれる部分の面積\(S\)について,次が成り立つ.
$$
S
=\frac{\sqrt{D}^5}{960a^4}
\hspace{10pt}
(D:=3b^2-8ac)
$$

注意. 上の公式の形から, その面積は, \(f(x)\)の1次以下の項の係数(すなわち\(d,e\)) には寄っていないこともわかる. これについて, 定数項の値(\(e\))が面積に影響を与えないのは, 平行移動によって面積が不変であることから明らかである. 1次の項の係数(\(d\))については, 下のPDFか, 4次関数の対称性 を参照していただきたい.
